Firefighters putting out tropical fire

Improving Human Resiliency in the Face of Natural Disasters

Contacts
Sponsor

National Science Foundation

Hurricanes routinely cause billions of dollars in damage, with the recent examples of Katrina and Harvey each exceeding $100 billion. Damage from Hurricane Katrina was so extensive that only 1/3 of the adults who evacuated New Orleans returned to their homes.Damage comes in many forms, typically from some combination of flooding, wind, and storm surge.

There are many factors that are important to families in deciding whether to evacuate in the face of an oncoming hurricane. These include household income, pets, type of home (e.g., mobile homes), and mobility of household members. It is important to understand the factors that are important to families in deciding to evacuate, and how those decisions are made and who evacuates. Furthermore, individuals/families that shelter in place (rather than evacuate) may find it difficult to find and procure basic necessities during and (immediately) after a hurricane.

There are two major thrusts for this on-going project. The first is to build an agent-based model to quantify the effects of different factors on the evacuation decision-making process. There are several factors that have been identified, but not quantified, and others that have not been studied. One important factor that we have studied is the fear of looting (theft and other crime) when too many people evacuate from a neighborhood. The second thrust is to identify and evaluate mechanisms for citizens to share resources during, and in the immediate aftermath of, a hurricane. As part of this second effort, we are building a web app for people to share information about available resources (what, where, how many).

We have studied the effects of looting concerns (i.e., crime) on families’ decisions to evacuate as a hurricane nears, using an agent-based model.

  1. Using survey data from Hurricane Sandy (that hit the northeastern US in 2012), we developed a bimodal model of social influence. We used that model to study the effects of looting on evacuation decision-making. Essentially, if the neighbors of a family evacuate, then that family will be more inclined to evacuate, owing to social influence. However, if too many neighbors of a family have evacuated, then that family is concerned about looting, and resists evacuating. We demonstrated through computations that concern over looting can reduce evacuation rates by up to 50%.
  2. A second work on looting included developing a more detailed model from statistical analyses of the survey data. We include family (household) factors such age, gender, race, and amount of schooling of head-of-household; type of housing; and numbers of vehicles. Neighbor influence includes the degree to which a household values the decisions of friends and neighbors, and how many of those neighbors have evacuated. A case study shows that if the police can allay citizens’ fears of looting, then evacuation rates can increase by as much as 50%. 3. Agent-based modeling can provide temporal insights about the dynamics of evacuation decision-making in a population.

Figures

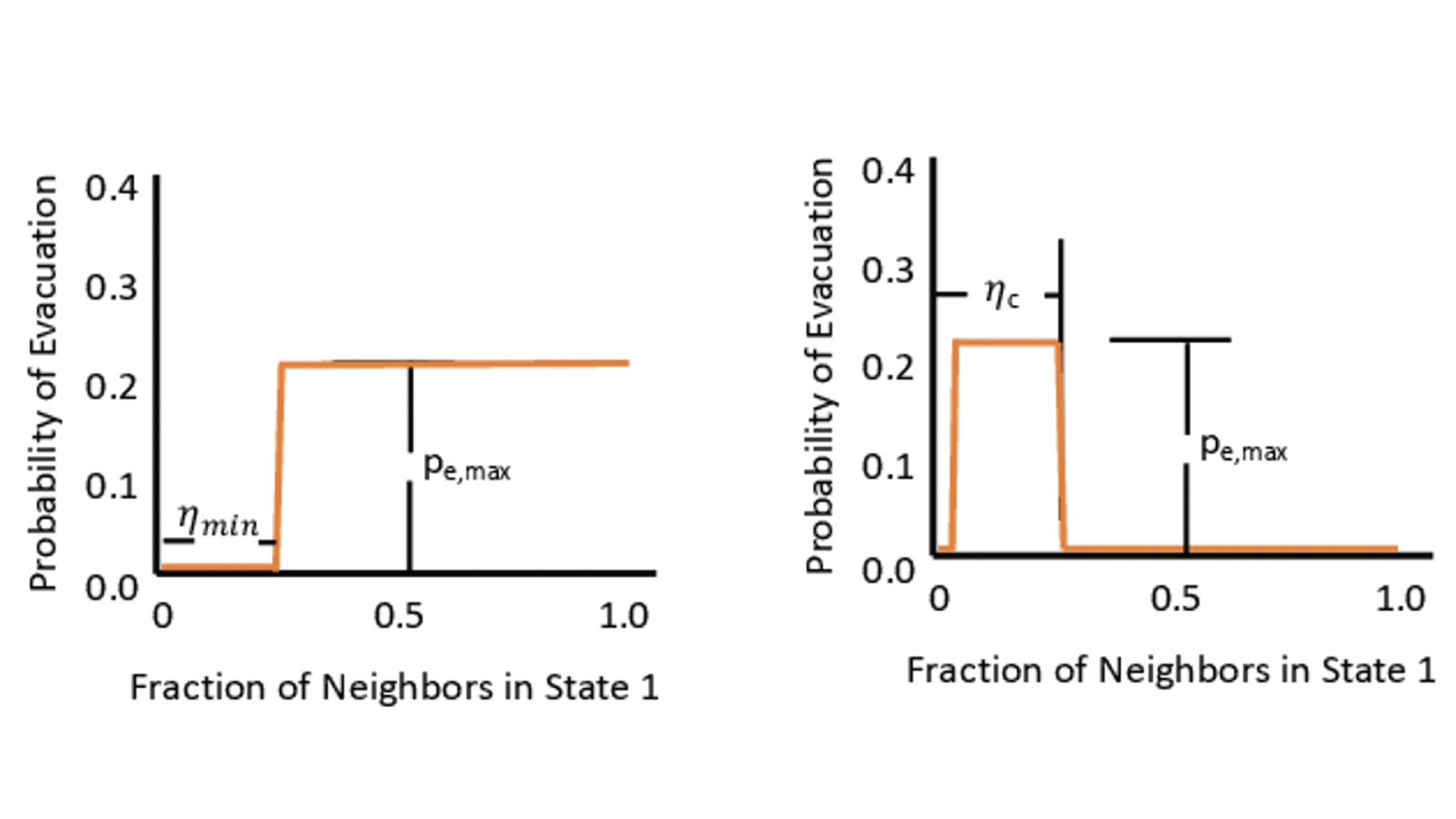
Graphs with yellow and black lines
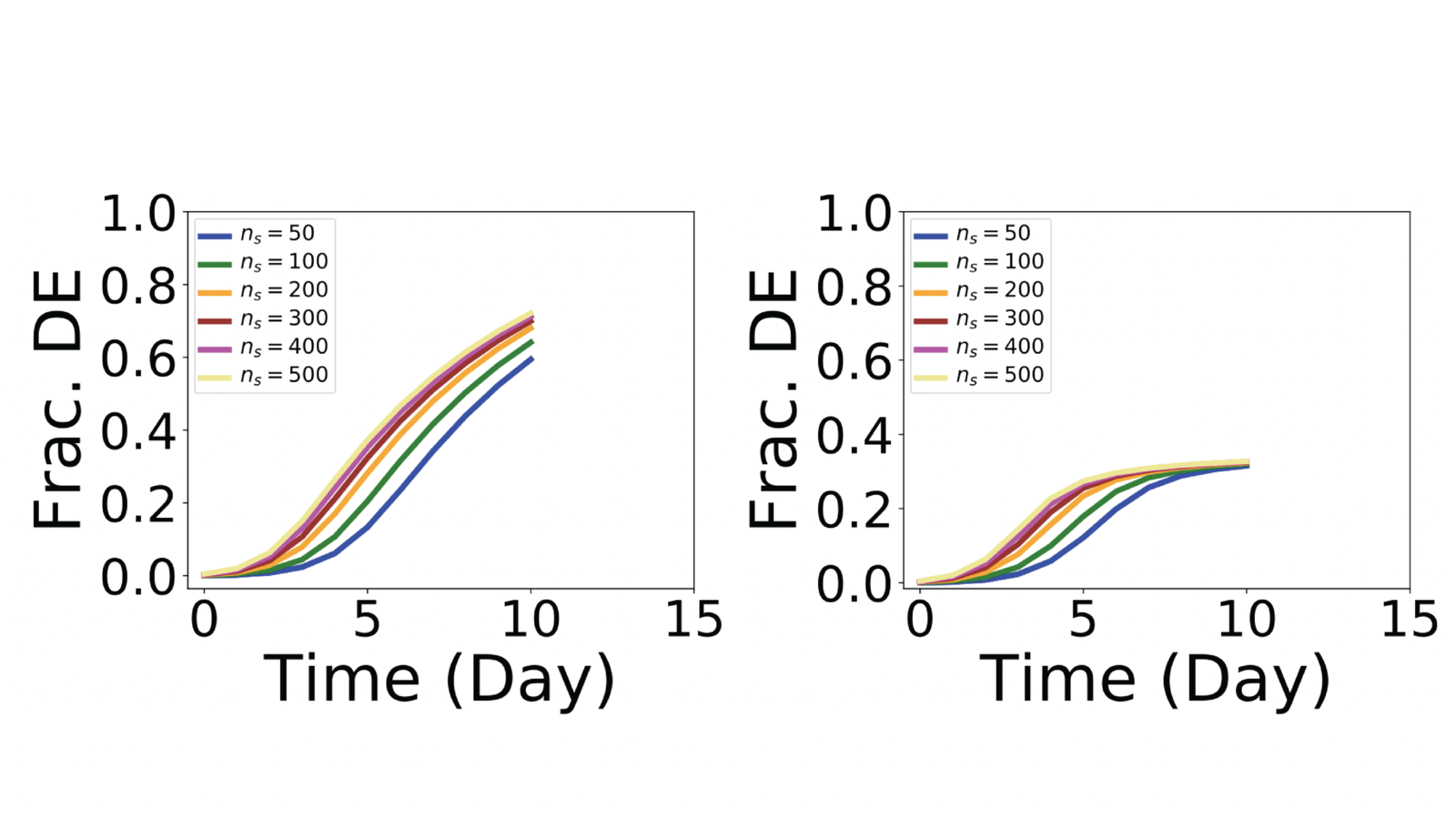
Graphs with rainbow upward trends
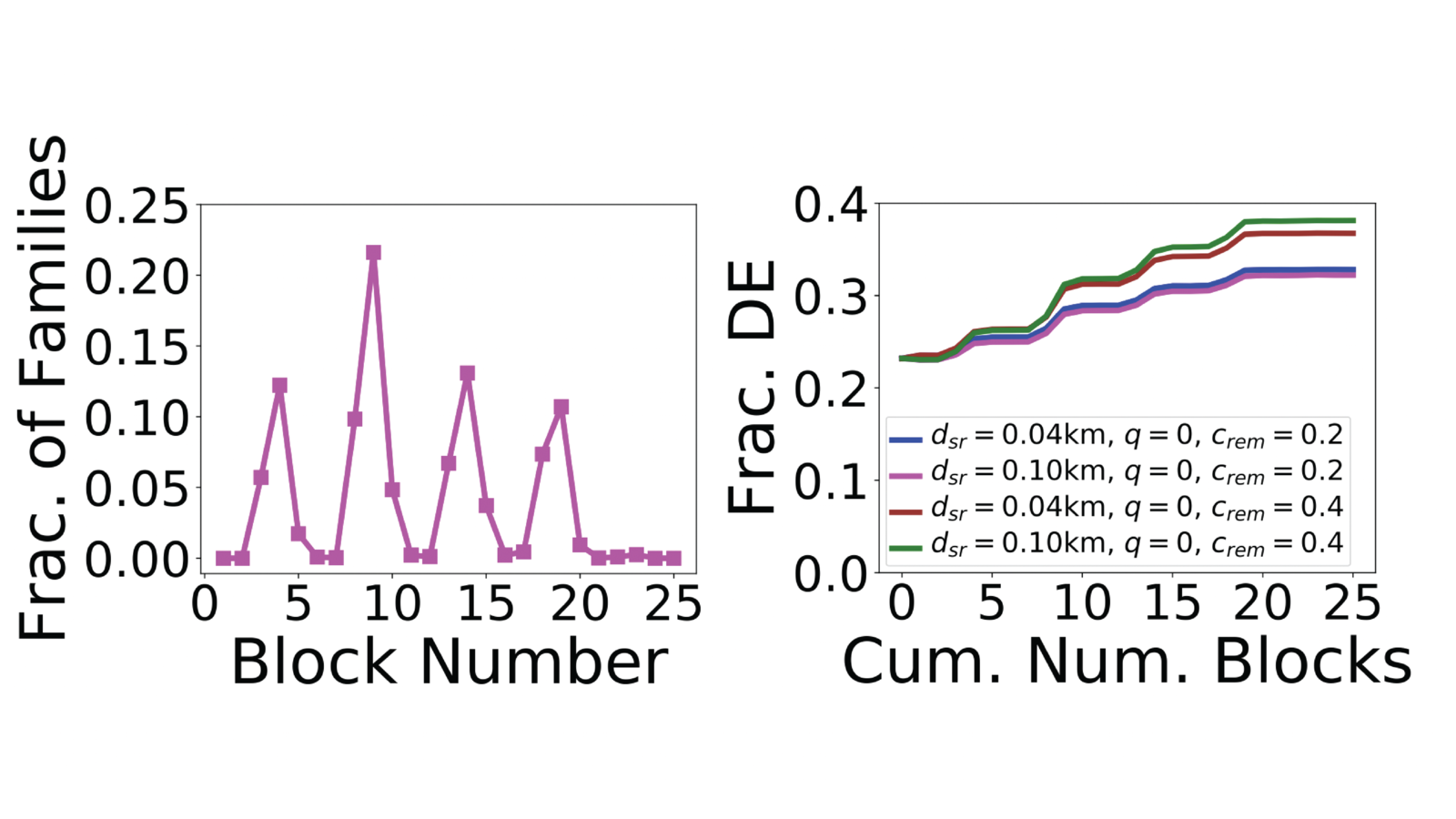
Graph with spiky pink line, and multiple upwards curvy lines

Figure 1. (Left) Classic influence model. As the fraction of neighbors evacuating increases, the probability of evacuation of a family is non-zero. (Right) Looting model. If the fraction of a family’s neighbors that are evacuating is too large, then the family will not want to evacuate.

Figure 2. (Left) Simulation results from the classic influence model. The cumulative fraction of families deciding to evacuate (Frac. DE) increases as the day of hurricane arrival nears (hurricane arrival is day 10). (Right) Simulation results from the looting model. The fraction of families evacuating plateaus at about 30%. Too many neighbors of a family have already evacuated, resulting in these families sheltering in place. The fraction of families evacuating decreases by roughly 50% compared to the resullts of the classic model. Different curves correspond to different numbers of families evacuating at the start of the simulations (i.e., at day 0 of the 10-day simulation).

Figure 3. This case study is that of police going house-to-house attempting to alleviate families’ concerns over looting and crime. Virginia Beach, Virginia is divided into a 5x5 grid (for 25 grid cells). Police travel from south to north, along each of the five columns of cells. (Left) This figure shows the fraction of total families visited in each of the 25 grid cells (the sum of all fractions is 1.0). The fractions “spike” in four places, since the northern region of Virginia Beach is most densely populated. (Right) Simulation results showing the fraction of families deciding to evacuate as a function of the cumulative number of blocks visited by police increases, in order 1 to 25, as indicated on the left. In the right plot, a stair-step increase in the fraction of evacuating families is observed as the police visit high-density regions. The different curves on the right correspond to different social network representations of Virginia Beach, VA.

Achla Marathe headshot

Achla Marathe

Professor

Professor of Public Health Sciences, School of Medicine

Anil headshot

Anil Vullikanti

Professor

Professor of Computer Science, School of Engineering and Applied Science

Network Systems Science and Advanced Computing
Conference Proceeding

Increasing Evacuation during Disaster Events

Kuhlman C; Marathe A; Vullikanti A; Halim N; Mozumder P . Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems. 2020; :654-662
Network Systems Science and Advanced Computing
Conference Proceeding

Two-Mode Threshold Graph Dynamical Systems for Modeling Evacuation Decision-Making During Disaster Events

Halim N; Kuhlman C; Marathe A; Mozumder P; Vullikanti A . International Conference on Complex Networks and Their Applications. Springer. 2019; :519-531